UP Board and NCERT Solution of Class 9 Science [विज्ञान] ईकाई 3 गति, बल तथा कार्य – Chapter-7 Motion (गति) दीर्घ उत्तरीय प्रश्न Dirgh Uttareey Prashn

प्रिय पाठक! इस पोस्ट के माध्यम से हम आपको कक्षा 9वीं विज्ञान ईकाई3 गति, बल तथा कार्य  के अंतर्गत चैप्टर7 (गति) पाठ के दीर्घ उत्तरीय प्रश्न प्रदान कर रहे हैं। UP Board आधारित प्रश्न हैं। आशा करते हैं कि पोस्ट आपको पसंद आयेगी अगर पोस्ट आपको पसंद आई तो इसे अपने दोस्तों के साथ में जरुर शेयर करें                        

Class	9th	Subject	Science (Vigyan)
Pattern	NCERT	Chapter-	Motion

दीर्घ उत्तरीय प्रश्न Dirgh Uttareey Prashn

प्रश्न 1. गति की सापेक्षता से क्या तात्पर्य है? उदाहरण देकर स्पष्ट कीजिए।

उत्तर-गति की सापेक्षता (Relativity of Motion)-ऐसी वस्तुएँ जिनमें समय-परिवर्तन के साथ, वस्तु की स्थिति का परिवर्तन होता है, गाति की अवस्था (state of motion) में कही जाती हैं।

इसके विपरीत, जिस वस्तु की स्थिति में समय के साथ परिवर्तन होता हुआ नहीं प्रतीत होता, उसे स्थिर अथवा विराम-अवस्था (state of rest) में कहा जाता है।

क्या जो वस्तु हमें स्थिर अथवा गतिमान प्रतीत होती है, वह वास्तव में उसी अवस्था में होती है ?

यदि हम चलती ट्रेन में बैठे हों तो हमें ट्रेन के बाहर की वस्तुएँ, जैसे पेड़- पौधे, घर आदि पीछे की ओर गति करते दिखाई देते हैं तथा हम ट्रेन को तथा स्वयं अपने को स्थिर देखते हैं। परन्तु वास्तविकता यह है कि ट्रेन के बाहर के पेड़-पौधे आदि अपने स्थान पर ही स्थिर होते हैं तथा हम ट्रेन के साथ गति कर रहे होते हैं।

अब यह कैसे निश्चित किया जा सकता है कि कौन-सी वस्तु गतिमान है तथा कौन-सी स्थिर ?

जब हम ट्रेन में बैठे होते हैं तो हमें बाहर की वस्तु, जैसे प्लेटफार्म गतिमान प्रतीत होता है तथा ट्रेन स्थिर। अब यदि हम प्लेटफार्म पर खड़े हों तो हमें प्लेटफार्म स्थिर तथा ट्रेन गतिमान प्रतीत होती है। इसका अर्थ यह है कि किसी वस्तु का गतिमान अथवा स्थिर दिखाई देना, देखने वाले की अपनी स्थिति पर निर्भर करता है। दूसरे शब्दों में यह कहा जाता है कि किसी वस्तु की गतिशीलता अथवा स्थिरता को प्रेक्षक के सन्दर्भ में ही बताया जा सकता है। प्रेक्षक को अपनी (गति अथवा स्थिरता की) अवस्था बदल जाने से, देखी जाने वाली वस्तु की गति अथवा स्थिरता की दशा बदल जाती है।

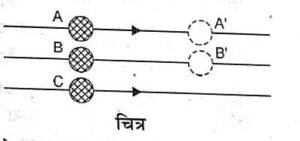
उदाहरण – चित्र में प्रदर्शित. तीन समान्तर मार्गों पर स्थित ट्रेनों में बैठे यात्रियों A, B एवं C पर विचार कीजिए। ट्रेनें A तथा B एक दिशा में समान चाल से चल रही हैं तथा ट्रेन C स्थिर है। इस दशा में-

(i) व्यक्ति C, व्यक्ति A तथा B को आगे जाते हुए देखेगा।

(ii) समान चाल से गति करने के कारण A तथा B की स्थितियों में समान परिवर्तन (A → A’ एवं B → B’) होगा। अतः A एवं B एक-दूसरे को निरन्तर साथ-साथ देखेंगे अर्थात् ये एक-दूसरे को स्थिर प्रतीत होंगे।

(iii) A एवं B व्यक्ति C को पीछे की ओर गति करते हुए देखेंगे। इसका यह अर्थ है कि व्यक्ति B, व्यक्ति A को स्थिर एवं व्यक्ति C को गतिमान देखेगा। इसी प्रकार A एवं B, स्थिर व्यक्ति C को पीछे की ओर गतिमान कहेंगे।

यदि ये तीनों व्यक्ति ट्रेनों के बाहर अन्य किसी वस्तु को न देख पायें तो यह नहीं निश्चित कर सकेंगे कि वास्तव में कौन गतिमान है तथा कौन स्थिर?

प्रश्न 2. उदाहरण देकर गति के प्रमुख प्रकार बताइए।

उत्तर- गति के प्रकार (Types of Motion)

1. ऋजुरेखीय गति (Rectilinear Motion)-जब कोई वस्तु किसी ऋजुरेखीय मार्ग पर एक ही दिशा में गति करती है तो उसकी गति को ऋजुरेखीय गति कहते हैं। उदाहरणतः ऊपर से नीचे गिरती हुई वस्तु की स्वतन्त्र गति, सीधी पटरी पर रेलवे ट्रेन की गति आदि।
2. वृत्तीय गति (Circular Motion)-इस प्रकार की गति में वस्तु किसी वृत्त की परिधि से बने मार्ग पर गति करती है। किसी घड़ी की सुई के नोंक की गति इसका प्रमुख उदाहरण है। किसी चक्र की परिधि पर स्थित किसी भी बिन्दु की गति भी वृत्तीय होती है।
3. दोलन गति (Oscillatory Motion)- इस प्रकार की गति में वस्तु अपने मार्ग के किसी निश्चित बिन्दु के इधर-उधर बारम्बार गति करती है। घड़ी के पेण्डुलम की गति, किसी झूले की गति आदि दोलन-गति के उदाहरण हैं।

प्रश्न 3. विस्थापन क्या है? यह दूरी से किस प्रकार भिन्न है?

उत्तर-विस्थापन-किसी निश्चित दिशा में वस्तु की स्थिति में हुआ परिवर्तन विस्थापन कहलाता है।

मान लीजिए, एक वस्तु मूल बिन्दु O से समय t₁ पर x₁ स्थिति में है और समय t₂ पर x₂ स्थिति में है।

अगर विस्थापन d है तो d = (x₁ – x₂).

विस्थापन का चिन्ह-विस्थापन की दिशा तीर (arrow-head) द्वारा प्रदर्शित करते हैं, जो मूल बिन्दु से अन्तिम स्थिति की तरफ खींचा जाता है, तीर (arrow-head) की लम्बाई विस्थापन का परिमाण (magnitude) प्रदर्शित करती है।

अगर विस्थापन मूल बिन्दु के दायीं तरफ है तो इसे धन चिन्ह (+) से व विस्थापन मूल बिन्दु के बायीं तरफ है तो इसे ऋण चिन्ह (-) से प्रदर्शित करते हैं।

दूरी-आम भाषा में विस्थापन व दूरी का एक ही अर्थ लिया जाता है, लेकिन विज्ञान में विस्थापन व दूरी में थोड़ा अन्तर है, “विस्थापन किसी वस्तु की स्थिति में किसी निश्चित दिशा में परिवर्तन कहलाता है जबकि दूरी वस्तु द्वारा उसकी अन्तिम स्थिति में पहुँचने में तय किये गये पथ की लम्बाई है।”

प्रश्न 4. (i) वेग-समय आरेख क्या प्रकट करता है?

(ii) समान वेग से गतिमान वस्तु का आरेख कैसा दिखाई देगा?

(iii) समान वेग 40 km/h की गति से चलती एक कार के लिए एक वेग-समय आरेख खीचिए।

उत्तर-

(i) सरल रेखा में गतिमान किसी वस्तु के लिए समय के साथ वेग में विभिन्नता को वेग-समय आरेख द्वारा दर्शाया जाता है। इस आरेख में समय को x अक्ष के साथ और वेग को -अक्ष के साथ दर्शाया जाता है।

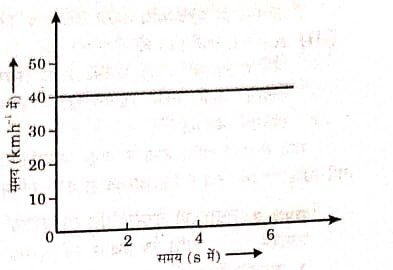
(ii) यदि वस्तु समान वेग से गतिमान होती है, तो समय के साथ इसके वेग-समय ग्राफ की ऊँचाई नहीं बदलेगी। यह x-अक्ष के समानान्तर एक सरल रेखा होगी।

(iii) 40 km/h के समान वेग से गतिमान एक कार का वेग-समय आरेख

प्रश्न 5. दूरी-समय ग्राफ क्या है? एकसमान तथा असमान गतियों के लिए एक ग्राफ खींचें। इस वक्त से नीचे वाला क्षेत्र क्या दर्शाता है? इसकी ढाल क्या बताती है?

उत्तर-दूरी-समय ग्राफ– समय को स्वतन्त्र चर अक्ष पर तथा दूरी को परतंत्र-चर अक्ष पर लेकर खींचा गया ग्राफ दूरी-समय ग्राफ कहलाता है। इससे हर क्षण पर दूरी का तथा इसकी ढाल से चाल का पता चल सकता है। दूरी-समय ग्राफ निम्न तीन प्रकार के हो सकते हैं-

(i) दूरी-समय ग्राफ जब चाल अपरिवर्तित रहती है-जब चाल अपरिवर्तित रहती है तो दूरी-समय ग्राफ एक सरल रेखा होती है। इसे चित्र में रेखा OA द्वारा प्रदर्शित किया गया है। दूरी-समय ग्राफ की किसी बिन्दु पर ढाल उसकी चाल बताती है।

(ii) दूरी-समय ग्राफ जब चाल एकसमान दर से बदलती हो– इस स्थिति में दूरी समय ग्राफ एक परवलय (Parabola) होती है। इसे चित्र में दिखाया गया है।

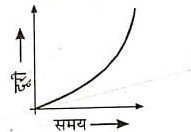
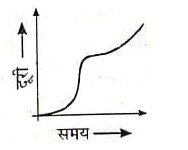
 (iii) दूरी-समय ग्राफ जब चाल असमान दर से बदलती हो– इस स्थिति में दूरी-समय ग्राफ एक सरल रेखा या परवलय न होकर एक वक्र रेखा होती हैं जिसका स्वरूप चाल बदलने की दर पर निर्भर करता है। इसे चित्र में दिखाया गया है।

प्रश्न 6. गति के प्रथम समीकरण v =u + at की व्युत्पत्ति कीजिए।

उत्तर-मान लीजिए किसी गतिमान पिण्ड का प्रारम्भिक वेग u तथा t समय पश्चात् उसका अन्तिम वेग v है तथा आरोपित त्वरण α है तो गति के समीकरण = u + at की व्युत्पत्ति करनी है।

चूँकि त्वरण = वेग परिवर्तन / समयान्तर

⇒     α = अन्तिम वेग – प्रारम्भिक वेग / समयान्तर

⇒     v-u = at

⇒      v=u+at                       इति सिद्धम्

प्रश्न 7. गति के द्वितीय समीकरण s= ut+1 + at² की व्युत्पत्ति 2 कीजिए।

उत्तर-मान लीजिए कि किसी गतिमान पिण्ड का प्रारम्भिक वेग u अन्तिम वेग v त्वरण α व तथा t समय में चली गई दूरी s हो तो गति के समीकरण s = ut + 1/2 at² की व्युत्पत्ति करनी है।

चूँकि प्रारम्भिक वेग u तथा v अन्तिम वेग है इसलिए औसत वेग = u+v/2 होगा।

चूँकि प्रारम्भ से 1 सेकण्ड बाद वेग = u + a एवं अन्तिम से 1 सेकण्ड पहले वेग = v- α  है।

प्रश्न 8. गति के तृतीय समीकरण = u + 2as की व्युत्पत्ति कीजिए।

उत्तर-मान लीजिए कि किसी गतिमान वस्तु का प्रारम्भिक वेग u, अन्तिम वेग v, त्वरण α, यात्रा में लगा समय t एवं कुल चली गई दूरी s हो, तो

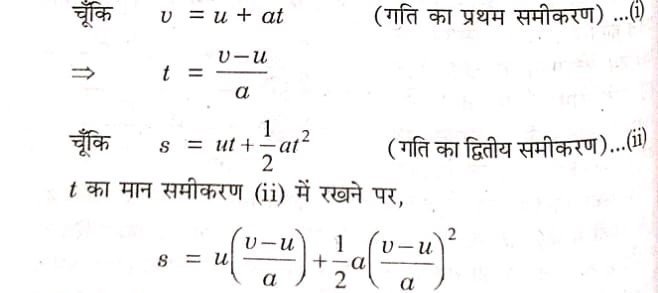
⇒   2as=2u (v-u) + (v-u)²

⇒    2as= (v-u) (2u+v-u)

⇒    2as= (v-u) (v + u)

⇒    2as= v² +u²

⇒     v² = u² + 2as

प्रश्न 9. एक वस्तु स्थिर अवस्था से चलना आरम्भ करती है। यदि वस्तु प्रथम 4 सेकण्ड में s₁ तथा अगले 4 सेकण्ड में s₂ दूरी तय करे, तो सिद्ध कीजिए s₁ = 3s₁.

उत्तर-वस्तु विरामावस्था से चलना आरम्भ करती है अतः

u = 0.

माना उसमें α त्वरण है अतः प्रथम 4 s में चली दूरी

S₁=1/2at² =1/2a(4)² =8a

कुल 8 सेकण्ड में चली s दूरी

s= 1/2 α (8)² = 32 α

अतः अन्तिम 4 सेकण्ड में चली दूरी

s₂ = s-s₁ =32 α-8 α = 24α.

इसलिए,                                                       s₂ = 3(8α)

या                                                                   S₂ = 3s₁

प्रश्न 10. (i) वृत्तीय गति क्या है? एक उदाहरण दीजिए।

(ii) समान वृत्तीय गति क्या है?

(iii) यदि एक धावक त्रिज्या वाले वृत्तीय पथ का एक r पूरा चक्कर लगाने में। समय लेता है तो वेग-विस्तार, त्रिज्या और समय के बीच सम्बन्ध ज्ञात कीजिए।

(iv) एक कृत्रिम उपग्रह पृथ्वी का एक पूरा चक्कर लगाने में 90 मिनट लेता है। उपग्रह की कोणीय गति का परिकलन कीजिए।

उत्तर-(i) एक वृत्तीय पथ के साथ-साथ किसी पिण्ड की गति वृत्तीय गति कहलाती है। वृत्तीय गति के दौरान, किसी निश्चित बिन्दु पर गति की दिशा को उस विन्दु पर स्पर्श रेखा डालकर जाना जाता है।

उदाहरण-

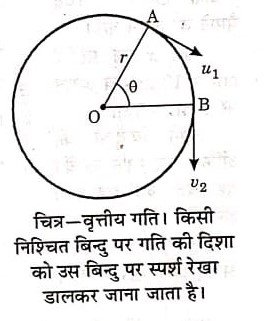
(a) पृथ्वी तथा अन्य ग्रह सूर्य के इर्द-गिर्द वृत्तीय पथ पर चक्कर काटते हैं। (b) चन्द्रमा भी पृथ्वी के इर्द-गिर्द वृत्तीय पथ पर गतिशील है।

(c) एक मजबूत धागे से बँधा पत्थर जब घुमाया/हिलाया जाता है, तो वह पत्थर भी वृत्तीय गति को संकेतित करता है।

(ii) जब कोई वस्तु एक वृत्तीय पथ के सापेक्ष समान चाल से गतिशील हो, तो इसे समान वृत्तीय गति कहते हैं।

(iii) वेग-विस्तार निम्न के द्वारा दिया जाता है-

V = 2πr/t

जहाँ

r = वृत्तीय पथ की त्रिज्या

t= वृत्तीय पथ का एक चक्कर लगाने में लगा समय

(iv) t=90 min (90 × 60) s

θ = 2π rad

= θ/t =2π/90*60

π/2700 rad

प्रश्न 11. कोई व्यक्ति 3 km की दूरी पूरब की ओर, फिर 2 km की दूरी उत्तर की ओर और 3.5 km की दूरी पूरब की ओर तय करता है। ज्ञात कीजिए-

(i) व्यक्ति द्वारा तय की गयी दूरी

(ii) उसकी स्थिति में विस्थापन।

उत्तर-(i) जैसा कि हम जानते हैं, दूरी किसी वस्तु द्वारा तय किये गये पथ की वास्तविक लम्बाई होती है।

अतः दूरी = 3 km + 2 km + 3.5 km = 8.5 km

(ii) विस्थापन या अन्तिम व आरम्भिक स्थितियों में अन्तर ज्ञात करने के लिए, एक सुविधाजनक स्केल (पैमाना) लेकर चित्र खींचते हैं।

माना 1 km = 1 cm

व्यक्ति 3 km पूरब जाता है, तब AB= 3 cm, BC = 2 cm उत्तर अर्थात् AB के लम्बवत् खींची फिर CD = 3.5 cm पूरब अर्थात् पुनः BC के लंम्बवत् खींची जैसा कि चित्र में प्रदर्शित है।

AD को मापकर देखो।

AD की लम्बाई = 6.8 cm …

विस्थापन = 6.8 km

प्रश्न 12. वृत्तीय और एकसमान वृत्तीय गति का वर्णन कीजिए।

उत्तर-

वृत्तीय गति-एक वृत्ताकार पथ पर किसी पिण्ड की गति वृत्तीय गति कहलाती है।

समान वृत्तीय गति-जब कोई पिण्ड किसी वृत्ताकार पथ पर समान चाल से गति करता है, तब यह गति समान वृत्तीय गति कहलाती है।

क्या समान वृत्तीय गति त्वरित गति है– वह गति एकसमान गति कहलाती है, यदि गति करने वाला पिण्ड किसी निश्चित दिशा में समान समय अन्तराल में समान दूरी तय करता है। यदि पिण्ड असमान दूरी तय करता है या दिशा बदलता है तो यह गति त्वरित गति कहलाती है।

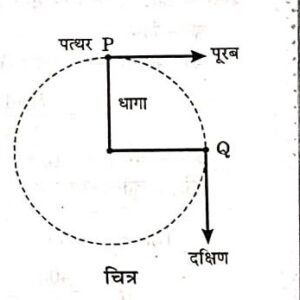
एकसमान वृत्तीय गति के विषय में, एक उदाहरण द्वारा उसे स्पष्ट करेंगे। एक छोटे पत्थर के टुकड़े को एक मजबूत धागे से बाँधकर उसे एक वृत्ताकार पथ पर एकसमान गति से घुमाते हैं, जैसा कि चित्र में प्रदर्शित है। जब पत्थर P बिन्दु पर है, और उसे छोड़ दिया जाये तो वह पूरब दिशा में गति करता है, और जब पत्थर Q स्थिति में है और उसे छोड़ा जाये तो वह दक्षिण दिशा में गति करता है।

अतः P व Q बिन्दुओं पर पिण्ड के गति करने की दिशा समान नहीं है इसीलिए पिण्ड का वेग तो समान है फिर भी दिशा में हर बिन्दु पर लगातार परिवर्तन होता है।

अतः समान वृत्तीय गति सदैव एक त्वरित गति है।